問題演習は単元の解説を確認するための問題なので、まずは解説を確認しておいてくださいね。
問題
問1
- 次の数を+、-の記号を用いて表しなさい。
(1)0より3大きい数
(2)0より2小さい数
(3)0より2.5大きい数
(4)0より{3/2}小さい数

問2
- 次の[]の数について、後の問いに答えなさい。
[-2,4,+2.3,{-4/5},0,{4/2},-0.01]
(1)[]内の負の数を全て選びなさい。
(2)[]内の整数を全て選びなさい。
(3)[]内の自然数を全て選びなさい。

問3
- 家を0、東の方向を正としたとき、次の位置を表しなさい。
![]()
(1)食堂の位置を数字で表しなさい。
(2)学校の位置を+、-の記号を用いて数字で表しなさい。
(3)公園の位置を+、-の記号を用いて数字で表しなさい。

問4
- 次のことがらを指示に従って表しなさい。
(1)東へ200m(-を用いて)
(2)東へ-100m(-を用いない)
(3)-10分前(-を用いない)
(4)10分後(-を用いる)
(5)5分前に戻るボタン(○分後の形を全て答えなさい)
(6)-15分後(○分前の形)


解答
問1
- 次の数を+、-の記号を用いて表しなさい。
(1)0より3大きい数
(2)0より2小さい数
(3)0より2.5大きい数
(4)0より{3/2}小さい数

と言う事で数直線上で、「0よりも3大きい(右)の数」や「0よりも2小さい(左)の数」を示してみましょう。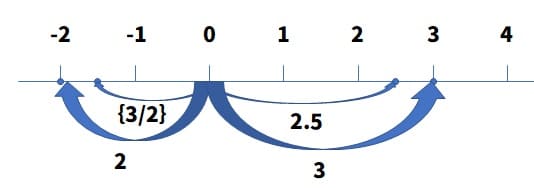
後は問題をよく読みましょう。
「+、-の記号を用いて表しなさい。」ですね。
「3」は「+3」と書かないといけません。
(1)+3
(2)-2
(3)+2.5
(4)-{3/2}
なお、(4)は「-」の位置を分数の前に着けて書くと良いです。
{-3/2}でも間違いではありませんけど、分数の中ではなく前に書いた方が、分数全体が-なんだとわかりやすいですね。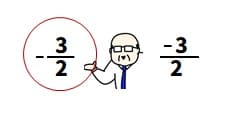

差が出る理解!
(4)の問題はよく「-1.5」という答えを書く子がいます。
間違いではないのですが・・・。
「数学」では小数よりも分数の方を好んで使います。
つまり、この(4)の答えはむしろ「-{3/2}」の方が好ましい答えです。
ただ、(3)の様に元から小数を使っているような問題は小数で答えます。
一方で計算する教科は他に「理科」がありますね。
こちらは分数よりも小数を好んで使います。
数学は「厳密に正しい世界」を求めるため、0.0001でも違っていれば基本的には間違いになります。
一方で理科には「大体あっていれば問題ない」を求めるため、小数を使います。
分数では直感的にわかりにくい数も、小数で書くと「大体どれくらい」か、わかりやすくなるからですね。
例えば{186325/8433}がどんな数字なのかぱっと見ただけではわかりにくいですね?
これは計算すると22.0947・・・という数になるのですが、理科では「22.1位までわかればいいじゃん!」の世界なんですね。

そもそも理科の世界で使われる計算式は「大体これくらい」という数量がほとんどです。
寸分の狂いもなくぴったり1gの分銅なんてありえませんし、分分の狂いもなくぴったり1cmの定規もありません。
さらに定規の線には太さがあるので、厳密にどこが1cmかなんてわかりようも無いですよね。
大体わかればそれでいいのが理科の世界であり、理科で不要に厳密な値を用いるのはナンセンスです。


ちゃんと解説するから戻るボタンはやめてね!
問2
- 次の[]の数について、後の問いに答えなさい。
[-2,4,+2.3,{-4/5},0,{4/2},-0.01]
(1)[]内の負の数を全て選びなさい。
(2)[]内の整数を全て選びなさい。
(3)[]内の自然数を全て選びなさい。

どの問題も、まず問題を理解しないことには問題は解けません。
問題に記載されている内容は理解しなければいけませんが、使われている用語を知らなければどうしようも無いですね。
※推測すれば解けなくは無いですが、確実に100点を取りたい場合のスタンスでは無いですね。
- 負の数:0より小さい数
- 整数:小数点以下の無い数
- 自然数:0より大きい整数
という事で、これに該当する数を「選べば」いいですね。
選ぶというのもポイントで、記載されている書き方で書く必要があります。
{4/2}は2ですが、この場合{4/2}で答える必要がありますので注意しましょう。
(1)は0より小さいすうですから、-のつく数を選べばいいので「-2,{-4/5},-0.01」が答えです。
(2)は小数点以下の無い数を選ぶので、「-2,4,0,{4/2}」が答えです。
(3)は(2)の中から0より大きい数を選べばいいので「4,{4/2}」が答えです。
なお、自然数を答える問題は「0」が悩む点になります。
逆に悩む点があるからこそ試験で問われやすいので、こういう問題は絶対に間違えないようにしましょう。
問3
- 家を0、東の方向を正としたとき、次の位置を表しなさい。
![]()
(1)食堂の位置を数字で表しなさい。
(2)学校の位置を+、-の記号を用いて数字で表しなさい。
(3)公園の位置を+、-の記号を用いて数字で表しなさい。

家の位置を0とし、東の方向を正とするそうなので、そのように数直線上に数字を書き込みましょう。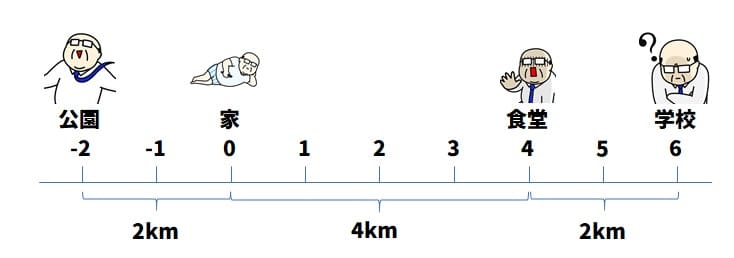

後は問題をよく読んで、答え方を確認しましょう。
(1)は「食堂の位置を数字で」なので「4km」もしくは「4」でも良いでしょう。
(2)は学校の位置を「+、-の記号を用いて」なので「+6km」もしくは「+6」でも良いでしょう。
(3)は公園の位置を「+、-の記号を用いて」なので「-2km」もしくは「-2」でも良いでしょう。
(2)のような問題は気を付けてくださいね。

問4
- 次のことがらを指示に従って表しなさい。
(1)東へ200m(-を用いて)
(2)東へ-100m(-を用いない)
(3)-10分前(-を用いない)
(4)10分後(-を用いる)
(5)5分前に戻るボタン(○分後の形を全て答えなさい)
(6)-15分後(○分前の形)

「(1)東へ200m(-を用いて)」ですが、まずはどうやって解いていくかのとっかかりが欲しい所ですね。

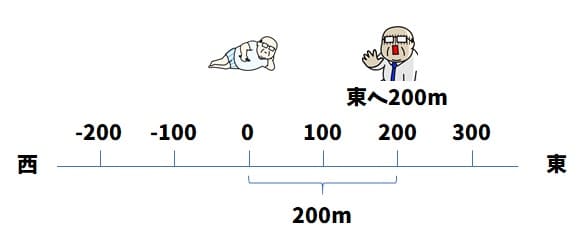
数直線を書くとこんな感じになりますね。
今回の問題の指示ですが、「東へ200m」を「-を用いて」となっています。
しかし、数直線上で東へ200mは正の数ですから、どうやっても-はつかないですよね・・・?

何故「東へ200m」が正の数となっているのか?
それは数直線上で東を正の方向としているからです。
このような数は、勝手に方向を考えて表しているので、正の方向の向きが暗黙に決まっているわけです。

東向きを正としているから東へ200mが正の数なので、東向きを負の数になるためには、西向きを正とすればいいですね?
数直線の向きを入れ替えます。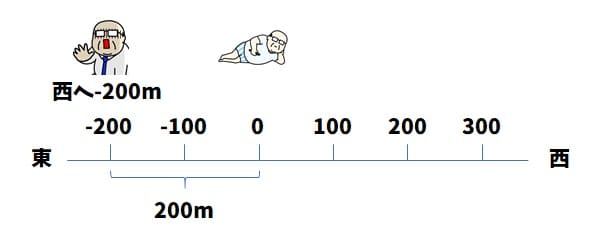
東へ200mの地点が左側、つまり負の数で表されます。
東へ200mは、西へ-200mと同じ意味ですね。
よって答えは「西へ-200m」です。
さて、この問題、ここで答えて終わりではもったいないですね。
「東へ200m」は「西へ-200m」と同じ意味と言う事を覚えておきましょう。
「東」という方向と「200」という数字、これを両方「逆向き」にするわけです。
何かをひっくり返して、更にひっくり返すと元に戻りますよね。
「東」の反対は「西」で、「200」の反対が「-200」、だから「東へ200m」と「西へ-200m」が同じ意味になるんですね。
次の問題はこれを使って解きましょう。
(2)は「東へ-100m」を「-を用いない」という指示に答えます。
「東へ-100m」は「東」を「西」に変えて、「-100」を「100」に変えた「西へ100m」と同じ意味です。
「西へ100m」は「-を用いない」に合っていますから、答えは「西へ100m」になります。
(3)の「-10分前」を「-を用いない」も同じように考えましょう。
「分前」の反対は「分後」、「-10」の反対は「10」で、「10分後」ですね。
答えは「10分後」です。
(4)は「10分後」を「-を用いる」ですが、これ、(3)の答えと問題の関係ですね。
答えは「-10分前」です。
(5)は「5分前に戻るボタン」を「○分後の形」で書きなさいという問題です。
しかも(○分後の形を全て答えなさい)という、今までにない指示です。

「5分前」は「前」を「後」にし、「5」を「-5」にして、「-5分後」と同じ意味ですね。
つまり「-5分後に戻るボタン」これが1つの正解です。
「1つの正解」というのは別の答えがあるからです。
問題にある「全て答えなさい」は「他に答えがありますよ」とも読み取れますね。

「前後」、「数字」、これ以外に反対にできる要素は他にないでしょうか?
「戻るボタン」・・・「戻る」これを反対にすると「進む」ですね。
「5分前に戻る」は「-5分前に進む」とも言えますし、「5分後に進む」とも言えます。
ただし答え方は「分後」ですから、「-5分前に進むボタン」は不適です。
「5分後に進むボタン」は問題に適した答えです。
よって、「-5分後に戻るボタン」、「5分後に進むボタン」の二つを答えるのが正解です。
(5)は「-15分後」を「○分前の形」という指示です。
「後」を「前」に変えなさいと言う指示ですから、「-15」も「15」に変えて、「15分前」で良いでしょう。